特征降维

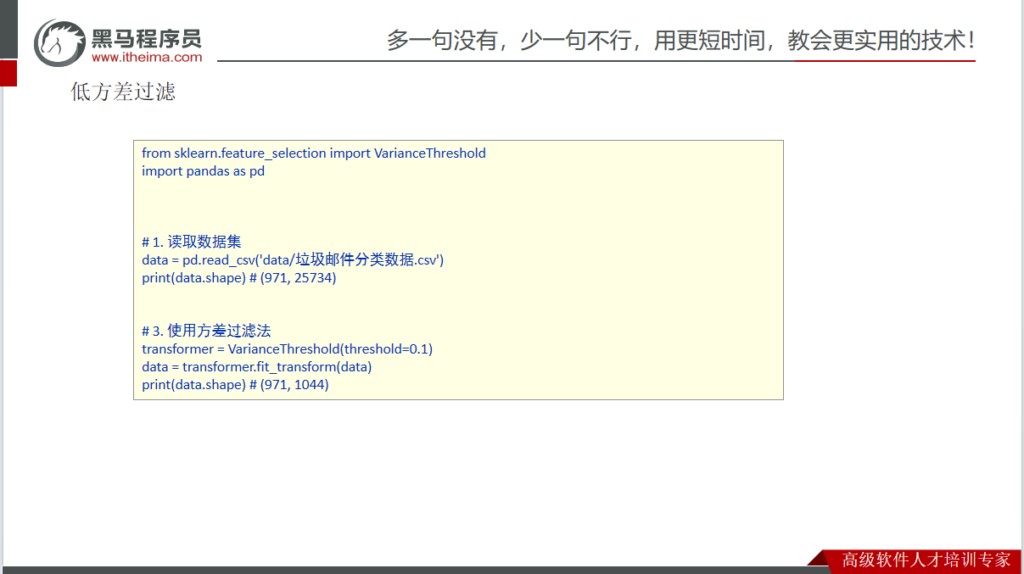
特征降维 – 低方差过滤法

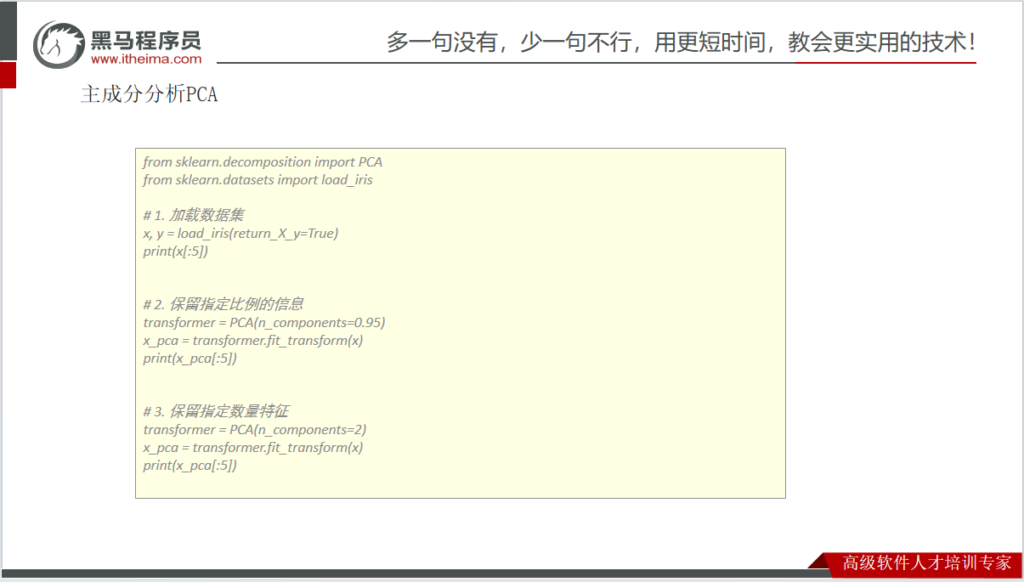
特征降维 – 主成分分析PCA

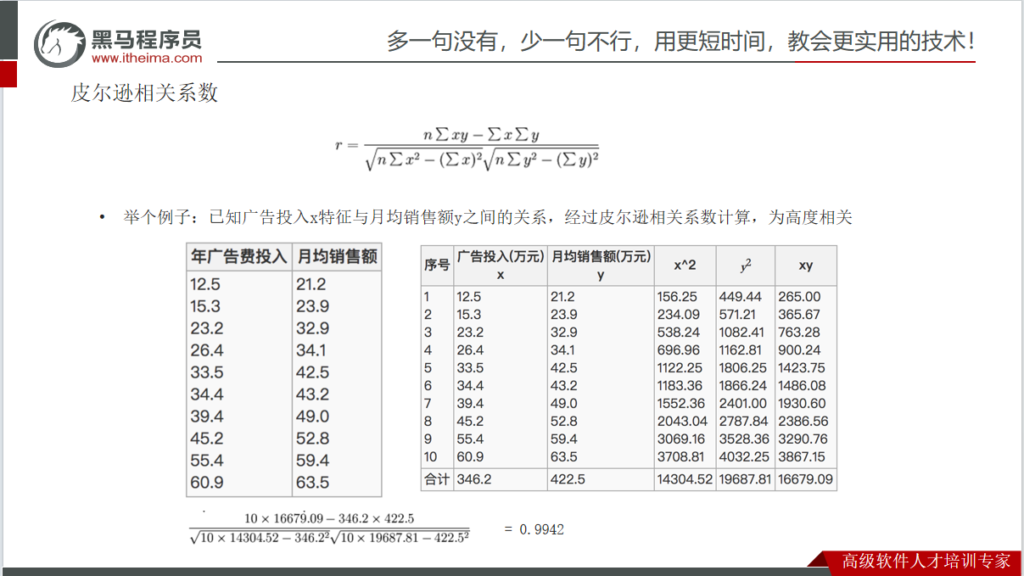
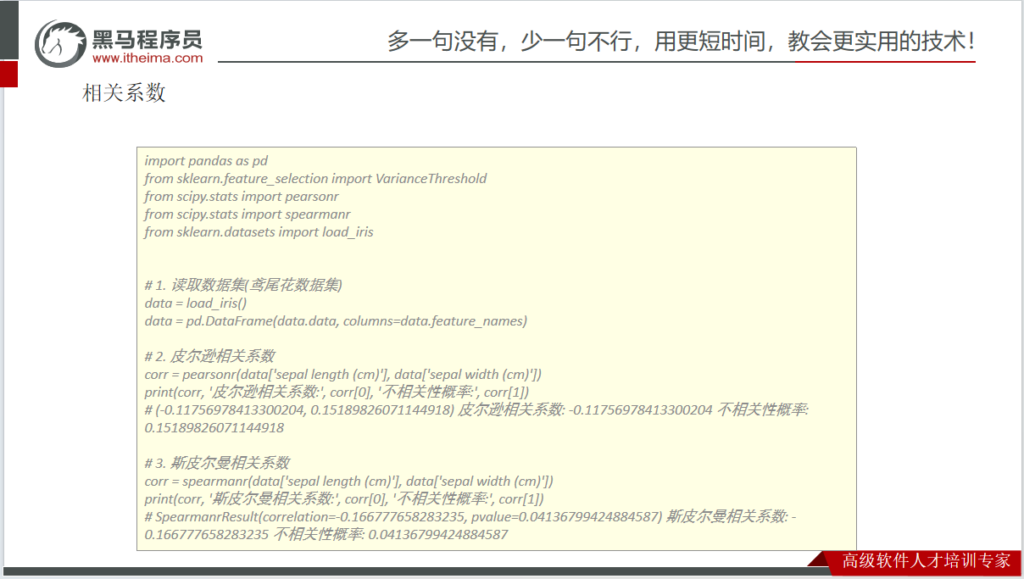
皮尔逊相关系数
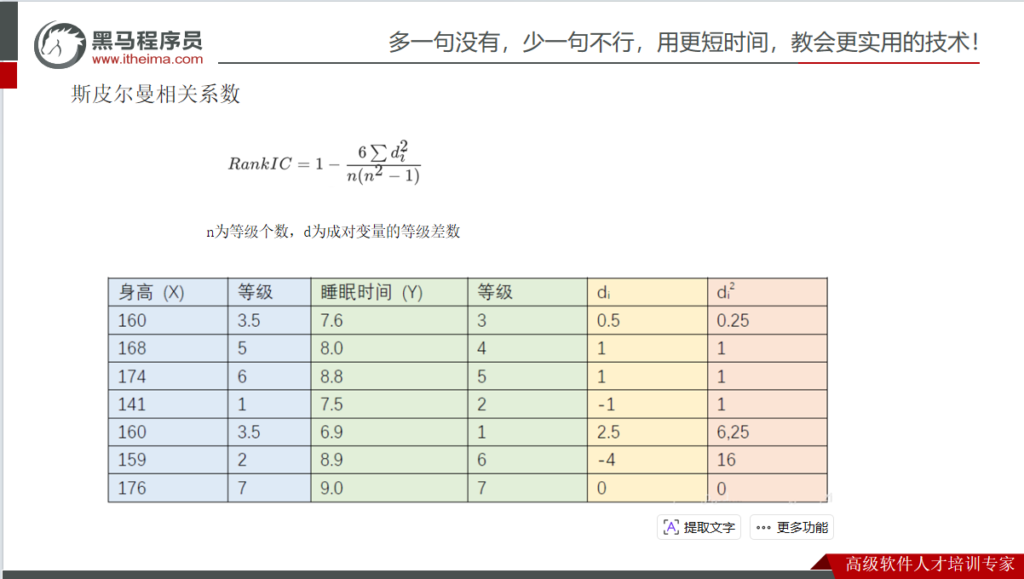
斯皮尔曼相关系数

特征降维示例代码
from sklearn.feature_selection import VarianceThreshold
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import pandas as pd
from scipy.stats import pearsonr,spearmanr
# 低方差过滤法
data = pd.read_csv('/root/data/titanic/ljyjflsj.csv')
print(data.shape)
transform = VarianceThreshold(threshold=0.1)
# 目的:创建一个方差阈值过滤器对象
# 参数解释:
# VarianceThreshold:sklearn中的特征选择类,用于移除低方差的特征
# threshold=0.1:设置方差阈值。方差低于0.1的特征将被移除
# 方差是衡量特征变化程度的指标:方差为0表示所有样本在该特征上取值相同
# 理解:相当于创建了一个"筛子",准备过滤掉不重要的特征
x = transform.fit_transform(data)
# 这是一个两步操作:
# fit(data):
# 计算每个特征的方差:分析输入数据data中每个特征列的方差
# 识别要删除的特征:标记方差 < 0.1 的特征
# 例如:如果data有100个特征,这一步会计算这100个特征的方差
# transform(data):
# 应用过滤:根据fit阶段计算的结果,移除方差低于阈值的特征
# 返回新数据集:只保留方差 ≥ 0.1 的特征
print(x.shape)
# pca
x,y = load_iris(return_X_y=True)
# return_X_y=True 表示分别返回特征矩阵x和标签向量y
print(x)
pca1=PCA(n_components=0.95)
print(pca1.fit_transform(x))
# PCA(n_components=0.95):创建一个PCA转换器,
# 当n_components是0到1之间的浮点数时,表示保留的方差比例
# fit_transform(x):
# fit:计算主成分方向(找到数据变化最大的方向)
# transform:将原始4维数据投影到主成分上,降维到能满足95%方差的最小维度
pca1=PCA(n_components=3)
# n_components=3:指定要保留的主成分数量
# 这里设置为3,意味着要将数据降到3维
# 原始鸢尾花数据是4维(4个特征),PCA会找到最能代表数据变化的3个新方向
print(pca1.fit_transform(x))
# 相关系数法
x,y = load_iris(return_X_y=True)
x1 = x[:,2]
# x[:, 2]:NumPy数组的切片操作
# 冒号::表示选择所有行(150个样本)
# 2:表示选择第3列(索引从0开始)
# 结果:提取所有样本的第三个特征(花瓣长度)
x2 = x[:,1]
# x[:, 1]:选择所有行的第2列(索引1)
# 结果:提取所有样本的第二个特征(花萼宽度)
print(pearsonr(x1,x2))
# PearsonRResult(
# statistic=np.float64(-0.4284401043305397),
# pvalue=np.float64(4.513314267273042e-08)
# )
# 结果解读:第一个值:负相关,且绝对值在0.43,是中等负相关
# 第二个值:远小于0.001,表示极高度显著
# 第一个值:相关系数 r
# 范围:-1 到 1
# 正值:正相关(一个增加,另一个也增加)
# 负值:负相关(一个增加,另一个减少)
# 接近0:无线性关系
# 接近±1:强线性关系
# 第二个值:p-value(p值)
# 范围:0 到 1
# 用于检验相关性的统计显著性
# 通常判断标准:
# p < 0.05:相关性显著
# p < 0.01:高度显著
# p < 0.001:极高度显著
print(spearmanr(x1,x2))
# SignificanceResult(
# statistic=np.float64(-0.30963508601557777),
# pvalue=np.float64(0.0001153938375056188)
# )
# 与pearsonr()类似,spearmanr()也返回一个包含两个值的对象:
# 第一个值:等级相关系数 ρ (rho)
# 范围:-1 到 1
# 正值:单调正相关(一个增加,另一个也增加)
# 负值:单调负相关(一个增加,另一个减少)
# 接近0:无单调关系
# 接近±1:强单调关系
# 第二个值:p-value(p值)
# 用于检验相关性的统计显著性
# 判断标准与皮尔逊相同